VOL.69【ミニ講座】(3)てんびん (4)三角形の合同条件
今この原稿を書いている部屋は非常に暑いです。
クーラーを入れればいいじゃないかと思うかもしれませんが、この部屋にはクーラーはありません。
扇風機を回すと紙が飛んでしまうので色々と書きながら作業する時は扇風機も回しません。
窓は開いていて風が入ってくればそれなりに涼しいのですが、ちょうど今は無風です。
パソコンがデスクトップなので移動することもできず、暑さとの闘いは今後も続きます。
解決策は
・エアコンを部屋につける
・ノートパソコンを買う
のどちらかでしょうが、果たして今年の夏に間に合うのか、自分でもわかりません。
決断力がないことがバレてしまいましたが、ミニ講座を頑張っていきたいと思います。
それでは【ミニ講座】のスタートです。
- 【ミニ講座】(3) てんびん
私は「てんびん」で解くのが大好きです。何よりもわかりやすいところが良いです!
通常は食塩水を混ぜるときに使うことが多いと思います。
「てんびん」でなぜ食塩水を混ぜたときの濃度が出るかというと、実はその正体が「平均」だからです。
ということは、「平均」を求めるような問題は全て「てんびん」が使えるので、「てんびん」が活躍する場面はかなり広いです。
「平均」は「面積図」が有効と言ってきましたが、それはあくまでイメージを掴むのに適しているという意味です。
解くためのツールと割り切るならば、「てんびん」の明快さに軍配が上がる場面も多いと思います。
ただ「てんびん否定派」も存在することは確かです。
彼らの言い分は『「面積図」も「てんびん」も結局一緒なのだからわざわざ2つもやることはない。』ということでしょう。
果たしてそうでしょうか。
中学受験の科目には「理科」もあります。
「理科」で「てこ」を習いますが、
『両端のおもりの重さと支点からの距離は「逆比」になる。』
という結論はかなり便利です。
そしてこれが「てんびん」そのものです。
ここで「てんびん否定派」の方々に聞きたいのですが、「理科」の「てこ」の問題も「面積図」で解くのですか?
また、「解法は少ないほど良い」という考え方は全ての問題を「方程式」で解くといった考え方につながっていきがちです。
その考え方は中学受験においては得策ではないことは前回の「消去算」のところで述べました。
「てんびん」も「面積図」もそれぞれ良いところがありますから、それを活かすことを考えるのが「算数」らしいやり方だと思います。「面積図」と「てんびん」をもう少し比べてみましょう。
- 描く手間は「てんびん」の方が簡単なので、わずかに「てんびん」が良し。
- 描く際のわかりやすさは、食塩水を混ぜるケースでは「てんびん」の方がわかりやすいと思いますが、問題によっては「面積図」の方が良いこともあるので、互角。
- ミスが出る可能性の低さでは「てんびん」がやや良し。
これは私の指導の経験から感じたものです。
ミスが多いのは「比」を逆にしてしまうケースです。
「面積図」の場合「縦」になっているものを「横」にする時に「左右」を間違えます。
「てんびん」はそもそも「左右」を入れ替えるので、そこさえ気をつければ大丈夫です。
ということで、「てんびん」が劣っているということは無さそうです。
受験生の皆さんは安心して「てんびん」を使ってもらいたいと思います。- 【ミニ講座】(4) 三角形の合同条件
「三角形の合同条件」は「数学(幾何)」で習います。「直角三角形の合同条件」も合わせると最も多くて以下の6つになります。
〈三角形〉
①3組の辺がそれぞれ等しい (三辺相等)
②2組の辺とその間の角がそれぞれ等しい (二辺夾角相等)
③1組の辺とその両端の角がそれぞれ等しい (二角夾辺相等)
④2組の角とその挟まれた辺以外の1辺がそれぞれ等しい(二角一対辺相等)
〈直角三角形〉
⑤斜辺と他の1辺がそれぞれ等しい(斜辺他一辺相等)
⑥斜辺と1つの鋭角がそれぞれ等しい (斜辺一鋭角相等)
まず、「受験算数」において「三角形の合同条件」は頭に入れておく必要があるかどうかについてですが、これは「必要である」ということで良いと思います。
「合同の発見」がテーマになっている問題がある以上、やらなければしょうがないのですが、小学生に上記の6つをそのまま教えても良いかどうか、悩ましいところです。
できればもう少し簡潔にまとめたい。
ということで、検討していきます。
まず④が怪しいです。
2つの角が等しければ残り1つの角も等しくなるので、③に帰結します。
③と④をまとめると以下のようになるでしょうか。
「2つの三角形の対応する2つの角と1つの辺がそれぞれ等しければ、その2つの三角形は合同である」
単に「2角と1辺が等しい」だけだと「相似」の可能性があるので、「対応する」が必要なんですね。このあたりのことをきちんと学ぶと「図形」の「力」がつくと思います。
また、⑥は④に含まれるので結局③に行き着きます。
2つ削れそうな感じにはなってきましたが、それがベストかどうか、もう少し検討します。
ここで、「2辺1対角相等」がなぜだめなのか考えてみます。
このケースは「角」の大きさが重要です。
結論を先に言うと
①鋭角→2通り考えられ、そのうちの1つは合同
②直角→合同
③鈍角→合同
75%以上の確率で合同となります。まぁ確率は関係ありませんけど(笑)
合同ではないケースがあるので、合同条件にはふくまれないんですね。ここからまとめに入ります。
2つの三角形の辺の長さと角の大きさを比べる際、まず、辺を3組と角を3組のセットにしてから比べます。
合計6組あるのですが、その6組全て等しい状況が合同を意味します。
実際は、そのうち3組が等しければ基本的には合同になります。
ただし、角は2組等しければ3組等しくなるので、角が3組等しいものは除きます。
合同にならない可能性があるケースは、辺が2組等しく、角が1組等しい場合です。
等しい角が辺にはさまれていれば合同です。
そうでないケースもその角が直角または鈍角の場合は合同になります。
等しい角が鋭角の場合は条件を満たす三角形が2つ(鋭角三角形と鈍角三角形)考えられ、そのうちのひとつは合同な三角形です。
小学生の場合は合同かどうかを確認するために「三角形の合同条件」を学ぶと思いますが、
「6つの要素のうち3つ同じならほぼ合同(例外も鋭角三角形・直角三角形・鈍角三角形の分類で同じところに入っていれば合同)」
という認識で十分なのではないでしょうか。
小学生らしさを活かす意味もあって、私はこのような結論を伝えています。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。中学受験ブログ ご質問フォーム
今週の基本2題割合・平面図形
難易度★★☆☆☆
- 3種類の食塩水A、B、Cがあります。
AとBを2:1の比で混ぜると9%の食塩水ができます。
BとCを3:2の比で混ぜると10.6%の食塩水ができます。
AとCを1:1の比で混ぜると13%の食塩水ができます。
AとBとCそれぞれの濃度を求めてください。 - 〈図1〉のような同じ大きさの三角定規がたくさんあります。
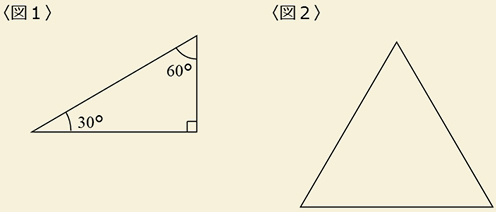
これらを組み合わせて正三角形を作ります。
〈図2〉は2枚を使って正三角形を作った様子です。
〈図2〉の正三角形がいちばん小さいとすると、小さいほうから10番目の正三角形を作るのに使用する三角定規は何枚ですか。
解答が表示されます













