VOL.8相似
昔「ルービックキューブ」という立体パズルがはやりました。
今でもご家庭で見かけることがあります。
私は立方体の積木の問題を見ると「ルービックキューブ」を思い出します。
立方体3×3×3=27(個)の積木ですから。
今は5×5×5のものや、正四面体、正十二面体まであるようです。
皆さんがお持ちでしたら、一度手に取ってみると良いかもしれませんね。
前回(ブログvol.7<4/28号>)の問題はさすがにパズルにはなっていないと思います。
でも、ありそうな形ですね。
それは「対称性」があるからで、問題文中にも「対称性のある美しい立体」というヒントらしきものを入れておきました。
では対称性とは何でしょうか?
簡単にいえば折り返したり、回転したり、鏡に映したりして元の図形と重なるような性質のことです。
小学生が習う「対称」は「線対称」「点対称 」の2つです。
これが立体になると、面に対して対称(鏡像対称)と軸に関して対称(回転体称)となります。
また、回転体称は180°回転して元の図形と重なるものだけでなく、90°や120°で重なるものも含みます。
立方体は回転軸が何本もあります。
90°回転して重なるものが3本、120°が4本、180°が6本です。
ルービックキューブ等の立方体を手に取って、いろいろ回して確認してくださいね。
ちなみに前回の問題に登場した立体『P』と『Q』の軸も立方体と同じだけあります。
今回は『拡大・縮小』について取り上げます。別の言葉でいえば『相似』です。
『相似』は平面図形の中で最重要テーマであるといえます。
また、数量の分野での重要テーマである『比』との結びつきも強く、入試対策としてかなり力を入れなければならないところでしょう。
まずは、ワンポイントアドバイスから。
| 拡大図・縮図 | 形が同じとはどういうことか理解しておきましょう。着目すべきポイントはほぼ3つで、①「中心点からの距離」・②「辺の長さ」・③「角の大きさ」です。①と②は対応するもの同士の比がそれぞれ等しければ、③は対応する角の角度がそれぞれ等しければ相似です。 |
|---|---|
| 縮尺 | 単位換算がからんできますので、少しでも不安がある場合は復習しておきましょ う。面積の場合は縮尺を2回掛けなければいけないことをお忘れなく。計算するときは分数を使い、いっぺんにやったほうが効率が良いです。 |
| 典型的な相似 | 平行線があれば三角形の相似が発生します。①「ピラミッド型」・②「砂時計型」の2つは押さえておきましょう。直角三角形も相似ができやすいので、典型的な形を頭に入れておきましょう。また、相似がなければつくるという積極性も必要で、「平行線をひく」「つの出し」等の技を身につけましょう。 |
| 台形への応用 | 台形は補助線を引いたほうが良いケースがほとんどで、そのパターンもほぼ2つです。1つは対角線で、1本で良い場合と2本引いたほうがよい場合があります。もう一つは台形の一方の脚に平行かつ頂点を通り台形の内部を通る線(2本あります)です。 |
押さえるべき基本事項はそれほど多くないのですが、出題のパターンは多種多様です。
全部を丸暗記することは事実上不可能ですから、典型的なものをしっかり頭に入れ、そこから先はそれを運用することを考えるべきでしょう。
算数の難しいところはどこまでを記憶で済ませるか、その加減だと思うのです。
目先のテストの点数を稼ぐにはできるだけ記憶に頼ったほうがよいのかもしれません。
ところが近年、学校側がそのような『パターン学習』に走った生徒はいらないという姿勢を打ち出しているケースが増えてきている気がします。
それは男子のトップ校で顕著であり、今後も続くものと思われます。
学校側が求めているのは『考える力』です。
この「相似」という分野は、基本をしっかり学び、それをもとに試行錯誤して正解にたどり着くという算数の「力」を養うのに最適な分野ではないでしょうか。
その上でテストの点数が良ければそれは『本物』です。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題相似
(図1)のように四角形ABCDは上底6cm、下底10cm、高さ10cmの台形です。
辺AB上に点Eをとったところ、三角形CDEの面積が42cm2になりました。
さらに(図2)のように2本の対角線を引きACとBDの交点をF、ACとEDの交点をGとします。
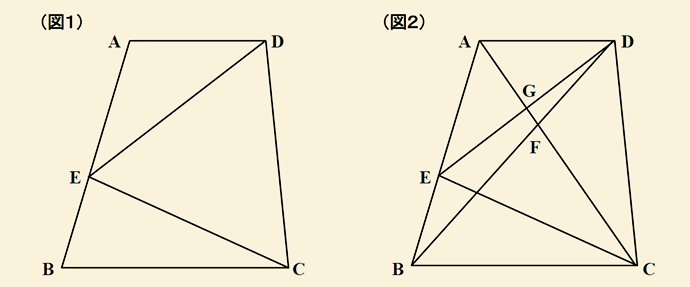
(1)AE:EBを求めてください。
(2)三角形DFGの面積を求めてください。
解答が表示されます













