VOL.6水
皆さん、あさイチは算数タイムに最適ですよ。
脳がフレッシュなうちに算数のトレーニングを積みましょう。
さて、前回(ブログvol.5<4/14号>)の問題ですが、いかがだったでしょうか。
解法の糸口が掴みにくかったかもしれませんね。
まず、純循環小数を分数であらわす場合、分母が9,99,999,・・・となることを知識にしておかないと苦しかったかもしれません。
算数は本来自分の頭で考えるべきだと思いますが、時間制限のある試験の対策としては、「知っている」で片づけられる範囲をひろげておく必要もあります。
実は前回の問題ではもう少し先まで知識にしておくことで、さらに時間が短縮できました。
それは「循環する数字の個数とそのようになる分数の分母の関係」です。例えば3個の数字が繰り返される場合、それを既約分数であらわしたときの分母は『「999」の約数かつ「9,99」の約数ではない数』となりますが、ここまでを知識にしておく訳です。
そして、その中で二桁のものは「27」と「37」であるというのはその場で考えて導き出せば十分です。
このテーマは以前6個の循環が開成で出題されました。
知識は大切ですが結論だけを丸暗記するのはやめましょう。
結論に至るまでの理論の積み重ねが力を養い、その力が得点の源になります。
「知識」は「力」を養う過程で獲得できる副産物と考えれば良いかもしれません。
今週のテーマは『立体図形』です。苦手にしている生徒さんが多い分野ではありますが、全ての問題に3次元的センスが要求されるわけではありません。
必要以上に恐れることもないでしょう。
テーマ別にポイントを挙げます。
| 見取図 | イメージをつかむには最適です。これがかければ一安心ですね。 |
|---|---|
| 展開図 | 頭の中で組み立てる練習をしましょう。当たり前ですが、表面積は展開図の面積と等しくなります。 |
| 投影図 | 立体を平面的にとらえる際の武器になります。斜めになっている面に気をつけましょう。 |
| 体積 | 体積を求めることができるのは「柱体」と「すい体」のみです。底面積と高さがわかれば後は計算問題ですね。 |
| 表面積 | 体積よりも面倒なことが多いです。「柱体」は公式がありますから必ず頭に入れておきましょう。複雑なものはできるだけまとめてから計算するのがコツです。また、直方体を組み合わせて作った立体は投影図を利用すればあっさりと求めることができます。 |
| 円すい | 公式が「体積」「展開図の側面のおうぎ形の中心角」「側面積」(「表面積」)と多いのでなぜそうなるのかを含めきちんと記憶しましょう。転がす問題は「回転数=母線÷底面の半径」を知識にしておきましょう。ひもを巻きつける問題は側面の展開図で考えます。 |
| 水 | 直方体の水そうの場合は平面で考えます。体積=面積×奥行とみて極力奥行は無視する方針でいきます。底面積が変化する問題も同様で、面積図で対応するようにしましょう。 |
今回取り上げたテーマのほとんどが、平面で考えて処理すれば解決できそうでした。
立体の攻略のカギは「いかに平面で考えるか」だと思います。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題水
(図1)のように直方体の水そうA(水そうの厚みはないものとします)と、直方体のおもりBがあります。水そうAには水が2.4L入っています。 おもりBの向きを変えて3回沈めたところ次のようになりました。 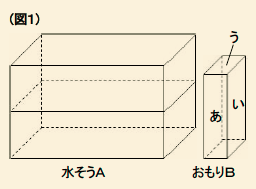
①「あ」の面を上にして沈めると、「あ」の面と水面の高さが等しくなり、その高さは10cmでした。 ② 次に「い」の面を上にして沈めると、「い」の面が水面より4cm下になりました。 ③ 次に「う」の面を上にして沈めると、②のときと比べて水位が2cm下がり、水そうA一杯に水を入れたときの水面と「う」の面は5cm離れていました。 (1)水そうAの底面積を求めてください。 (2)水そうAの容積を求めてください。
解答が表示されます













