VOL.184【受験お役立ち情報】 -最高レベルの算数実例-
今回は本文がそれなりのボリュームになったので、いきなり本題に入ります。
◎「応用」レベルの方針
皆が目指す領域ですね。算数がこのゾーンに達していれば好きな学校を受けることが可能と思われます。
ただ、トップレベルの成績を取っているとしても得手不得手というものはあるものです。
得意を伸ばすのか。弱点を補うのか。志望校が求めている能力に合わせるのか。自分に適正のある学校を受けるのか。悩みは尽きません。
ここまで昇り詰める受験生は皆個性が強い傾向にあります。そこで、私が過去に教えた生徒さんがどんなタイプでどのように成長したか、実例をいくつか紹介したいと思います。
①勤勉タイプ
低学年から徹底的に鍛えてきた生徒さんです。3年生時には全範囲を終え、中堅校レベルの入試問題なら解けるだけの実力がありました。私は5年生の終盤から指導しましたが、塾のテストは模試を含めほとんど偏差値70以上だったと記憶しています。強味は基本がしっかりしていることでした。
既視感がある問題はいとも簡単に正解します。計算ミスもほとんどありません。何か精密機械のようなイメージですが、それでも完璧ではありませんでした。
問題文の読み取りにはかなり難がありましたし、初見の問題には弱いところがありました。また、図形も弱いわけではないのですが、わからない(気が付かない)範囲が少し広いようにも感じました。
さて、これらの難点を克服するために何をやったかというと、なるべく初見の問題に多く触れるようにしました。時には私が問題を作ったりもしました。
また、書き出しが必要な学校を受ける予定だったので、その練習もかなりやりました。絵を描くときは全体の構成が大切だと思いますが、書き出しも同じです。「形」をしっかり身につけました。
最終的には、相当な難易度まで対応できるようになっていました。私がイメージしていたよりも安定度が高くなっていたようです。
②直観タイプ
「ちょっかん」の漢字を「直感」にするか「直観」にするか迷いました。調べてみると、「過去の記憶と結び付けてひらめく」のは「直観」が適しているようなので、こちらにしました。
この生徒さんはこの「結び付ける」能力が素晴らしく、特に「図形」を活かすことに長けていました。
彼が瞬間的にノートに描いた方法を、今も私の授業で取り入れたりしています。
では彼は完璧だったかというとそうでもなく、ミスもそこそこありましたし、知識に関しても量が不足気味でした。
なぜそんな状態だったかというと、大して努力をしないのにそれなりの成績を取れてしまうため、本来必要な努力を怠ってしまっていたのです。
私以外の先生から良く叱られていましたが、その時の彼はどこ吹く風と聞き流しているようでした。
私は子供は直接叱ってもあまり効果がないと考えているので、授業中はあまりうるさいことは言わないことにしています。
基本的には一人の人間として認め、本人の自覚に任せるというのが私のスタイルです。
ただし、それは放置しているのではなく、昔ながらの師弟関係を踏襲しているのです。職人さんがよく「技は盗むもの」といったことを言います。子供にはまわりにいる人間をコピーする能力が備わっているので、狭い空間を共有するだけで授業は十分に成り立っていると思うのです。
ただし、本人がそこにいる人間を“師”と認めないといけません。男子の場合は自分よりも優れていると感じた人を“師”と認めます。
1対1のスパーリングのような授業で私の“強さ”を吸収してもらう。
これで、彼の学力は盤石なものとなりました。
③改善タイプ
この生徒さんは前回の「上級レベル-数量優位」がピッタリの生徒さんでした。指導を始めた当初は算数だけが弱点で他の3教科はトップレベルという状態でした。これは責任重大だと思いながら指導を始めたのを覚えています。
まず私が強調したのが「計算の工夫」です。「数量優位」の受験生は多少の面倒は気にせずモリモリ計算することが多いので、「それはやめましょう」という私からのメッセージでした。
多少レベルの高いものまで、なぜそうなるのかを含め解説したのを覚えています。
(例)
・(A+B)×(A-B)=A2-B2
※VOL.95を参照してください。
・65×65は→6×(6+1)=42,5×5=25より4225
※VOL.93を参照してください。
これらを利用して
6512×6488
=(6500+12)×(6500-12)
=42250000-144
=42249856
このような解説をすればほぼ全ての生徒さんは理解して納得します。ところがしばらくしてこれと同じやり方が使える問題に出くわしたとき、使える人と使えない人に別れてしまいます。
使えない人は忘れてしまうのでしょうが、私はこれは心構えにあると思うのです。スポーツを例にすると、野球の守備に似ています。
例えばサードを守っていてボーっと立っているだけだと、強烈なサードゴロは取れないだけでなく危険な位です。やはり腰を落として構え、バッターのスイングを注視していなければ対応できないでしょう。
その意味ではこの生徒さんは心構えがしっかりしていました。習ったものが使えるときは絶対に使ってやるという強い意志を感じました。
私との授業をきっかけに、当然のように「数量優位」が解消され、むしろ「図形優位」なタイプになっていきました。
最終的にはほぼ最高のパフォーマンスを発揮できるようになるまでに成長してくれました。
今回は3人の実例を見てもらいました。トップクラスの受験生は皆個性が強いですから、志望校との兼ね合いでどのような着地を目指すのかという戦略が大切だと思います。
時には私のイメージを超える成長をみせてくれる受験生もいます。そんな時は私も最高の喜びを感じることができます。受験生の皆さんに感謝です。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題場合の数・立体図形
難易度:★★☆☆☆
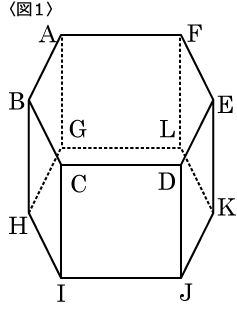
〈図1〉の立体は底面が正六角形の角柱です。
また、BDとDIの長さが等しくなっています。
A~Lの12個の点からいくつかの点を選んで図形を作ることを考えます。
(1)4つの点を結ぶと正方形が出来るような選び方は何通りありますか。
ただし、正方形ができない場合は0通りとして下さい。
(2)3つの点を結ぶと二等辺三角形ができるような選び方は何通りありますか。
解答が表示されます













